Overview

This assignment extends the model developed for HW0x04 to derive the controller gain values for the ball-plate system. There were four new sections added:

Deriving the K values symbolically from a 4th order generic characteristic polynomial for a closed loop system.
Finding the pole locations using 2 arbitrarily chosen pole locations (negative), an arbitrary natural frequency of the system, and an arbitrary damping ratio, for which another 4th order generic characteristic polynomial is created.
Calculating the K values by equating the polynomials from the prior 2 steps, and solving for the gain values. Additionally, the calculated gain values are double checked using Matlab's Control System toolbox.
Finally, the system response with the new gain values is plotted.

Simulation Results and Performance

The closed loop results from HW0x04, for comparison with the tuned system response from HW0x05

The tuned closed loop response for the following gain values: K = [-5.7941 -1.5335 -1.5612 -0.1296]

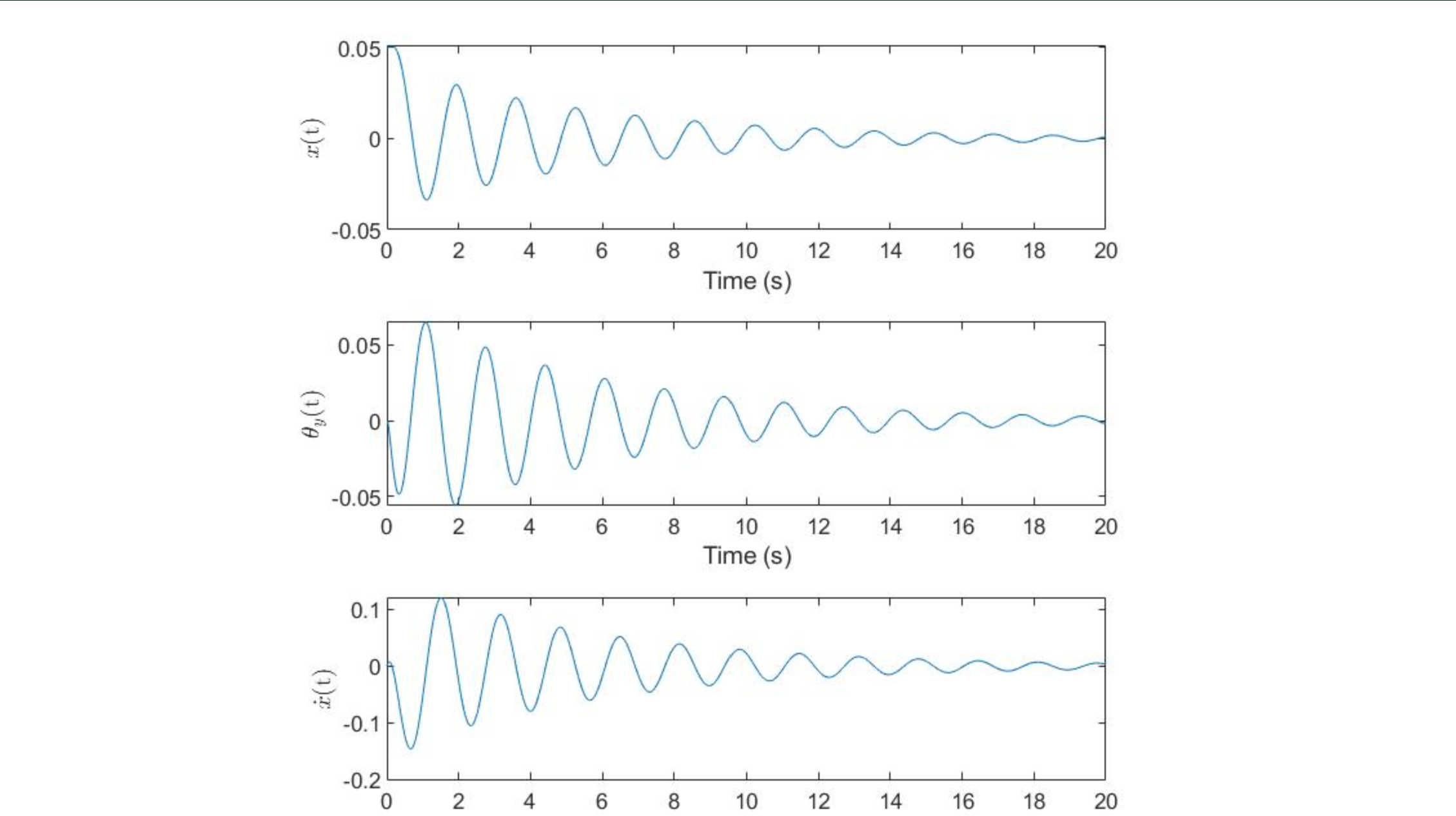
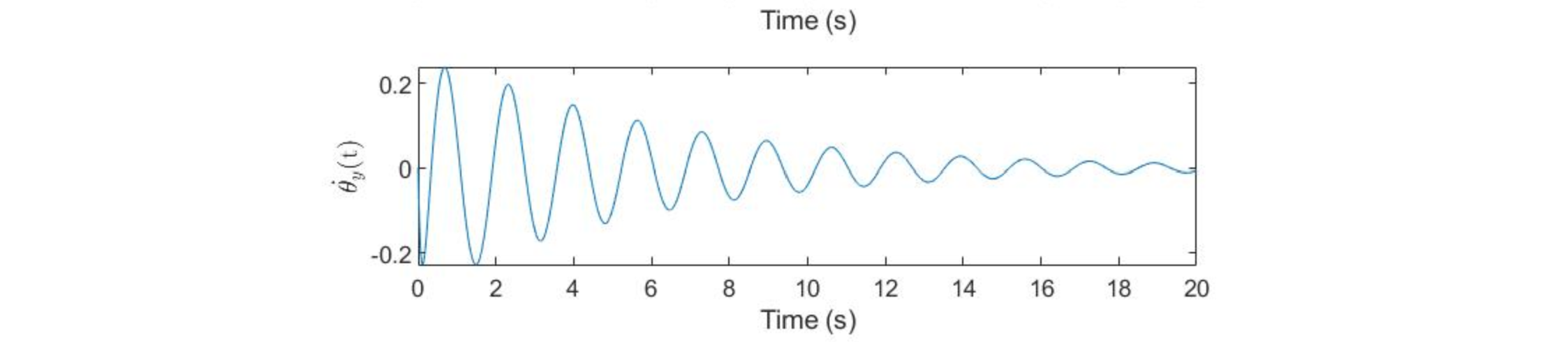
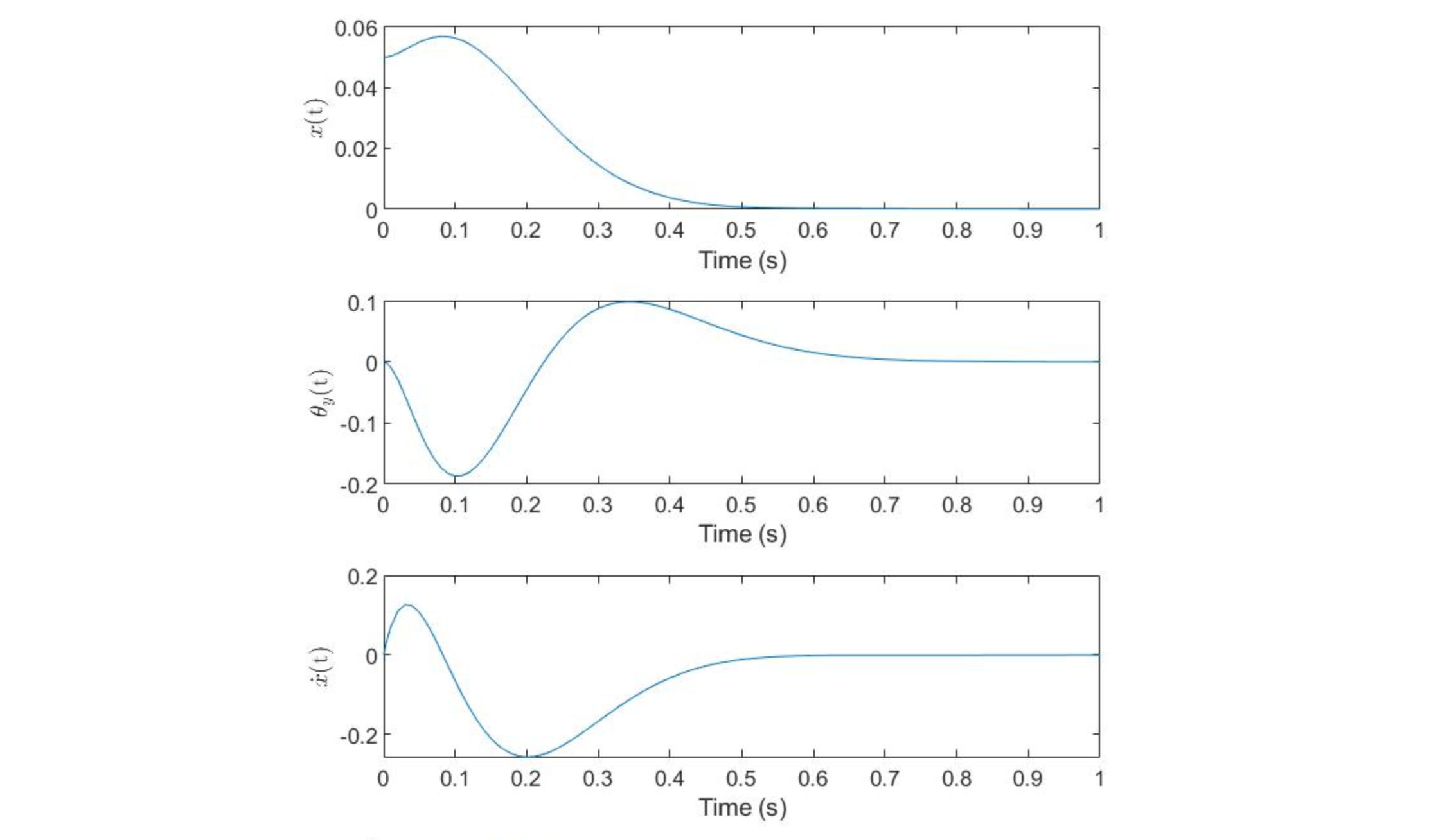
Note the significantly lower timescale of the response from the calculated k values (~0.6s to steady state) when compared to the response from the given k values (~15s to steady state)- this is much more ideal for the platform because the ball will be balanced in about 3 "tilts" rather than almost 20 "tilts." This will reduce the load on the motors when balancing the ball, and will allow the system to respond dynamically to various new stimuli, like a hand moving the ball after balancing, or the platform getting hit, causing the ball to move. Additionally, the maximum angle of tilt for the calcualted k values (~11 degrees), while greater than the maximum angle of tilt for the given k values by about 3 times, is still reasonably small such that the linear state space model remains accurate. Additionally, the angular velocity of the platform, while much greater for the calculated k values, is still low enough (in magnitude) at maxima and minima that the platform should be able to handle these speeds.

Source Code

For more information on the implementation of this process as well as the simulink model and foundational Matlab code used in this assignment, please visit this link: https://bitbucket.org/npatel68/me405_labs/src/master/hw5/

Author: Group 2: Neil Patel, Jacob Burghgraef

Date: May 16, 2021